| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 3 (Before Exercise 6.1) | Exercise 6.1 | Example 4 to 6 (Before Exercise 6.2) |
| Exercise 6.2 | ||
Chapter 6 Lines And Angles
Welcome to the comprehensive solutions guide for Chapter 6, "Lines and Angles," from the latest Class 9 NCERT mathematics textbook designed for the academic session 2024-25. This chapter builds significantly upon foundational geometric concepts learned in earlier classes, delving into a more rigorous exploration of the relationships between angles formed by intersecting lines and, crucially, by a transversal intersecting parallel lines. Mastering these concepts is essential for developing deductive reasoning skills and forming the bedrock for proving theorems in geometry. These solutions provide detailed, logical explanations and step-by-step methods for tackling the exercises effectively.
The chapter begins by reinforcing fundamental concepts related to angles formed by intersecting lines. The solutions revisit and clarify:
- Adjacent Angles: Sharing a common vertex and a common arm.
- Linear Pair of Angles: Adjacent angles whose non-common arms form a straight line, reinforcing that they are supplementary (sum to $180^\circ$).
- Vertically Opposite Angles: Formed when two lines intersect. A key aspect emphasized in the solutions is the proof that vertically opposite angles are always equal, demonstrating early deductive reasoning.
The core focus shifts dramatically to the scenario involving Parallel Lines and a Transversal. This interaction creates specific pairs of angles with predictable relationships, which are fundamental to Euclidean geometry. The solutions meticulously define, identify (using diagrams), and explain the properties associated with:
- Corresponding Angles: Located in matching positions at each intersection.
- Alternate Interior Angles: Located between the parallel lines and on opposite sides of the transversal.
- Alternate Exterior Angles: Located outside the parallel lines and on opposite sides of the transversal.
- Consecutive Interior Angles (Co-interior Angles): Located between the parallel lines and on the same side of the transversal.
Conversely, the chapter also deals with proving lines parallel. The solutions explain and apply the converse theorems: if a transversal intersects two lines such that a pair of corresponding angles are equal, OR a pair of alternate interior angles are equal, OR a pair of consecutive interior angles are supplementary, then the two lines must be parallel. These converse theorems provide the tools needed to justify parallelism in geometric proofs. Furthermore, the solutions provide a formal deductive proof for the Angle Sum Property of a Triangle (the sum of the three interior angles of any triangle is $180^\circ$), often utilizing the concepts of parallel lines and alternate interior angles. This fundamental property is then applied extensively in problems involving finding missing angles within triangles. The related Exterior Angle Theorem (an exterior angle of a triangle is equal to the sum of the two interior opposite angles) might also be revisited or applied in certain problems.
Regarding the rationalized syllabus for 2024-25, Chapter 6, "Lines and Angles," in the Class 9 NCERT textbook retains its core focus on fundamental angle relationships, properties related to parallel lines and transversals (and their converses), and the proof and application of the angle sum property of a triangle. The rationalization process primarily involved streamlining the complexity and number of exercises, potentially removing some highly intricate proofs or multi-step problems, ensuring students gain a solid understanding of the essential theorems and their applications in deductive reasoning. By diligently working through these detailed solutions, students can learn to apply geometric theorems rigorously, significantly enhance their logical deduction skills for finding angles, and master the techniques required for proving lines parallel.
Example 1 to 3 (Before Exercise 6.1)
Example 1. In Fig. 6.9, lines PQ and RS intersect each other at point O. If ∠ POR : ∠ ROQ = 5 : 7, find all the angles.

Answer:
Given:
Lines PQ and RS intersect at point O.
$\angle POR : \angle ROQ = 5 : 7$
To Find:
The measures of all angles: $\angle POR$, $\angle ROQ$, $\angle SOQ$, and $\angle POS$.
Solution:
From Fig. 6.9, we observe that the line segment PQ is a straight line. Angles $\angle POR$ and $\angle ROQ$ lie on this line and are adjacent angles forming a linear pair.
Therefore, the sum of these angles is $180^\circ$ (Linear Pair Axiom).
$\angle POR + \angle ROQ = 180^\circ$
The ratio of $\angle POR$ to $\angle ROQ$ is given as $5 : 7$. Let the common ratio be $x$.
So, let $\angle POR = 5x$ and $\angle ROQ = 7x$.
Substitute these into the linear pair equation:
$5x + 7x = 180^\circ$
Combine the terms on the left side:
$12x = 180^\circ$
Solve for $x$ by dividing both sides by 12:
$x = \frac{180^\circ}{12}$
$x = 15^\circ$
Now we can find the measures of $\angle POR$ and $\angle ROQ$:
$\angle POR = 5x = 5 \times 15^\circ = 75^\circ$
$\angle ROQ = 7x = 7 \times 15^\circ = 105^\circ$
Next, we use the property of vertically opposite angles. When two lines intersect, the vertically opposite angles are equal.
$\angle SOQ$ is vertically opposite to $\angle POR$.
$\angle SOQ = \angle POR = 75^\circ$
$\angle POS$ is vertically opposite to $\angle ROQ$.
$\angle POS = \angle ROQ = 105^\circ$
Thus, the angles are:
$\angle POR = 75^\circ$
$\angle ROQ = 105^\circ$
$\angle SOQ = 75^\circ$
$\angle POS = 105^\circ$
Verification:
Check if the sum of angles around point O is $360^\circ$: $75^\circ + 105^\circ + 75^\circ + 105^\circ = 360^\circ$. (Correct)
Check linear pairs: $\angle POR + \angle ROQ = 75^\circ + 105^\circ = 180^\circ$ (Correct). $\angle ROQ + \angle SOQ = 105^\circ + 75^\circ = 180^\circ$ (Correct). $\angle SOQ + \angle POS = 75^\circ + 105^\circ = 180^\circ$ (Correct). $\angle POS + \angle POR = 105^\circ + 75^\circ = 180^\circ$ (Correct).
Example 2. In Fig. 6.10, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠ POS and ∠ SOQ, respectively. If ∠ POS = x, find ∠ROT.

Answer:
Given:
Line POQ.
Ray OS stands on line POQ.
Ray OR bisects $\angle POS$.
Ray OT bisects $\angle SOQ$.
$\angle POS = x$
To Find:
The measure of $\angle ROT$.
Solution:
Since ray OS stands on line POQ, $\angle POS$ and $\angle SOQ$ form a linear pair.
The sum of angles in a linear pair is $180^\circ$.
$\angle POS + \angle SOQ = 180^\circ$
$\angle POS + \angle SOQ = 180^\circ$
(Linear Pair Axiom)
We are given that $\angle POS = x$. Substitute this into the equation:
$x + \angle SOQ = 180^\circ$
Solve for $\angle SOQ$:
$\angle SOQ = 180^\circ - x$
Ray OR bisects $\angle POS$. This means OR divides $\angle POS$ into two equal angles: $\angle POR$ and $\angle ROS$.
$\angle ROS = \frac{1}{2} \angle POS$
$\angle ROS = \frac{1}{2} x$
(OR is the angle bisector of $\angle POS$)
Ray OT bisects $\angle SOQ$. This means OT divides $\angle SOQ$ into two equal angles: $\angle SOT$ and $\angle TOQ$.
$\angle SOT = \frac{1}{2} \angle SOQ$
$\angle SOT = \frac{1}{2} (180^\circ - x)$
(OT is the angle bisector of $\angle SOQ$)
We want to find $\angle ROT$. From the figure, $\angle ROT$ is the sum of $\angle ROS$ and $\angle SOT$.
$\angle ROT = \angle ROS + \angle SOT$
Substitute the expressions for $\angle ROS$ and $\angle SOT$:
$\angle ROT = \frac{1}{2} x + \frac{1}{2} (180^\circ - x)$
Factor out $\frac{1}{2}$:
$\angle ROT = \frac{1}{2} (x + 180^\circ - x)$
Simplify the expression inside the parenthesis:
$\angle ROT = \frac{1}{2} (180^\circ)$
Calculate the final value:
$\angle ROT = 90^\circ$
Thus, the measure of $\angle ROT$ is $90^\circ$, regardless of the value of $x$. This is a general result: the angle formed by the bisectors of a linear pair is always $90^\circ$.
The value of $\angle ROT$ is $90^\circ$.
Example 3. In Fig. 6.11, OP, OQ, OR and OS are four rays. Prove that ∠ POQ + ∠ QOR + ∠ SOR + ∠ POS = 360°.
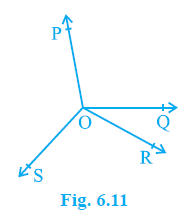
Answer:
Given:
OP, OQ, OR and OS are four rays originating from the point O.
To Prove:
$\angle$ POQ + $\angle$ QOR + $\angle$ SOR + $\angle$ POS = $360^\circ$.
Construction Required:
Produce ray OQ backwards to a point T so that TOQ is a straight line.
Proof:
Since ray OP stands on the straight line TOQ, the sum of adjacent angles forms a linear pair.
$\angle$ TOP + $\angle$ POQ = $180^\circ$
(Linear pair axiom) ... (1)
Similarly, since ray OS stands on the straight line TOQ, the sum of adjacent angles forms a linear pair.
$\angle$ TOS + $\angle$ SOQ = $180^\circ$
(Linear pair axiom) ... (2)
We can see from the figure that the angle $\angle$ SOQ is the sum of angles $\angle$ SOR and $\angle$ QOR.
$\angle$ SOQ = $\angle$ SOR + $\angle$ QOR
Substitute this into equation (2):
$\angle$ TOS + ($\angle$ SOR + $\angle$ QOR) = $180^\circ$
$\angle$ TOS + $\angle$ SOR + $\angle$ QOR = $180^\circ$
... (3)
Now, add equation (1) and equation (3):
($\angle$ TOP + $\angle$ POQ) + ($\angle$ TOS + $\angle$ SOR + $\angle$ QOR) = $180^\circ$ + $180^\circ$
$\angle$ TOP + $\angle$ POQ + $\angle$ TOS + $\angle$ SOR + $\angle$ QOR = $360^\circ$
... (4)
From the figure, the angle $\angle$ POS is the sum of angles $\angle$ TOP and $\angle$ TOS.
$\angle$ TOP + $\angle$ TOS = $\angle$ POS
Substitute $\angle$ POS for ($\angle$ TOP + $\angle$ TOS) in equation (4):
$\angle$ POS + $\angle$ POQ + $\angle$ SOR + $\angle$ QOR = $360^\circ$
Rearranging the terms to match the required statement:
$\angle$ POQ + $\angle$ QOR + $\angle$ SOR + $\angle$ POS = $360^\circ$
This shows that the sum of all angles around the point O is $360^\circ$.
Hence Proved.
Exercise 6.1
Question 1. In Fig. 6.13, lines AB and CD intersect at O. If ∠ AOC + ∠ BOE = 70° and ∠ BOD = 40°, find ∠ BOE and reflex ∠ COE.

Answer:
Given:
Lines AB and CD intersect at O.
$\angle$ AOC + $\angle$ BOE = $70^\circ$
$\angle$ BOD = $40^\circ$
To Find:
$\angle$ BOE and reflex $\angle$ COE.
Solution:
Since lines AB and CD intersect at O, the vertically opposite angles are equal.
Therefore,
$\angle$ AOC = $\angle$ BOD
(Vertically opposite angles) ... (i)
We are given that $\angle$ BOD = $40^\circ$.
From (i), we get:
$\angle$ AOC = $40^\circ$
We are also given that $\angle$ AOC + $\angle$ BOE = $70^\circ$.
Substitute the value of $\angle$ AOC in the given equation:
$40^\circ$ + $\angle$ BOE = $70^\circ$
Subtract $40^\circ$ from both sides:
$\angle$ BOE = $70^\circ - 40^\circ$
$\angle$ BOE = $30^\circ$
Now, consider the straight line AB. The angles on a straight line sum up to $180^\circ$.
Therefore,
$\angle$ AOC + $\angle$ COE + $\angle$ BOE = $180^\circ$
(Angles on a straight line) ... (ii)
We know $\angle$ AOC = $40^\circ$ and $\angle$ BOE = $30^\circ$. Substitute these values into equation (ii):
$40^\circ$ + $\angle$ COE + $30^\circ$ = $180^\circ$
$70^\circ$ + $\angle$ COE = $180^\circ$
Subtract $70^\circ$ from both sides:
$\angle$ COE = $180^\circ - 70^\circ$
$\angle$ COE = $110^\circ$
The reflex angle $\angle$ COE is the angle greater than $180^\circ$. It is calculated by subtracting the angle $\angle$ COE from $360^\circ$.
Reflex $\angle$ COE = $360^\circ - \angle$ COE
Reflex $\angle$ COE = $360^\circ - 110^\circ$
Reflex $\angle$ COE = $250^\circ$
Thus, $\angle$ BOE = $30^\circ$ and reflex $\angle$ COE = $250^\circ$.
Question 2. In Fig. 6.14, lines XY and MN intersect at O. If ∠ POY = 90° and a : b = 2 : 3, find c.
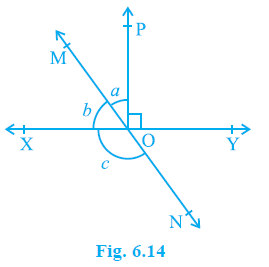
Answer:
Given:
Lines XY and MN intersect at O.
Ray OP stands on line XY such that $\angle$ POY = $90^\circ$.
The ratio of angles a and b is a : b = 2 : 3, where a = $\angle$ MOP and b = $\angle$ MOX.
To Find:
The value of c, where c = $\angle$ NOX.
Solution:
Since XY is a straight line, the sum of the angles on this line is $180^\circ$. The angles $\angle$ XOM, $\angle$ MOP, and $\angle$ POY are on the line XY.
$\angle$ XOM + $\angle$ MOP + $\angle$ POY = $180^\circ$
(Angles on a straight line)
Substitute the given values: $\angle$ XOM = b, $\angle$ MOP = a, and $\angle$ POY = $90^\circ$.
b + a + $90^\circ$ = $180^\circ$
Subtract $90^\circ$ from both sides:
a + b = $180^\circ - 90^\circ$
a + b = $90^\circ$
... (i)
We are given the ratio a : b = 2 : 3. Let a = $2x$ and b = $3x$ for some variable $x$.
Substitute these values into equation (i):
$2x + 3x = 90^\circ$
$5x = 90^\circ$
Divide both sides by 5 to find the value of $x$:
$x = \frac{90^\circ}{5}$
$x = 18^\circ$
Now we can find the values of a and b:
a = $2x = 2 \times 18^\circ = 36^\circ$
b = $3x = 3 \times 18^\circ = 54^\circ$
Now consider the straight line MN. Ray OX stands on line MN.
The angles $\angle$ MOX and $\angle$ NOX form a linear pair.
$\angle$ MOX + $\angle$ NOX = $180^\circ$
(Linear pair axiom)
Substitute the values: $\angle$ MOX = b and $\angle$ NOX = c.
b + c = $180^\circ$
Substitute the calculated value of b = $54^\circ$:
54$^\circ$ + c = $180^\circ$
Subtract 54$^\circ$ from both sides to find the value of c:
c = $180^\circ - 54^\circ$
c = $126^\circ$
Answer:
The value of c is $126^\circ$.
Question 3. In Fig. 6.15, ∠ PQR = ∠ PRQ, then prove that ∠ PQS = ∠ PRT.

Answer:
Given:
$\angle PQR = \angle PRQ$
To Prove:
$\angle PQS = \angle PRT$
Proof:
Ray QP stands on the line ST.
Therefore, $\angle PQS + \angle PQR = 180^\circ$ (Linear Pair Axiom)
This implies $\angle PQS = 180^\circ - \angle PQR$
$\angle PQS = 180^\circ - \angle PQR$
... (i)
Similarly, ray RP stands on the line ST.
Therefore, $\angle PRQ + \angle PRT = 180^\circ$ (Linear Pair Axiom)
This implies $\angle PRT = 180^\circ - \angle PRQ$
$\angle PRT = 180^\circ - \angle PRQ$
... (ii)
We are given that $\angle PQR = \angle PRQ$.
$\angle PQR = \angle PRQ$
(Given)
From (i) and (ii), since the right-hand sides are equal ($180^\circ$ minus equal angles), the left-hand sides must also be equal.
Therefore, $\angle PQS = \angle PRT$
Question 4. In Fig. 6.16, if x + y = w + z, then prove that AOB is a line.

Answer:
Given:
$x + y = w + z$
To Prove:
AOB is a line.
Proof:
We know that the sum of all angles around a point is $360^\circ$.
Therefore, at point O, we have:
$x + y + z + w = 360^\circ$
We are given that $x + y = w + z$.
$\text{Given, } x + y = w + z$
... (i)
Substitute $(w + z)$ with $(x + y)$ in the equation $x + y + z + w = 360^\circ$:
$(x + y) + (x + y) = 360^\circ$
$2(x + y) = 360^\circ$
Divide both sides by 2:
$x + y = \frac{360^\circ}{2}$
$x + y = 180^\circ$
Since $\angle BOC = x$ and $\angle COA = y$ are adjacent angles and their sum $\angle BOC + \angle COA = x + y = 180^\circ$, the non-common arms OA and OB form a straight line.
By the converse of the Linear Pair Axiom, if the sum of two adjacent angles is $180^\circ$, then the non-common arms form a straight line.
Thus, AOB is a straight line.
Question 5. In Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that
∠ ROS = $\frac{1}{2}$ (∠ QOS – ∠ POS).

Answer:
Given:
POQ is a straight line.
Ray OR is perpendicular to line PQ ($\angle POR = \angle ROQ = 90^\circ$).
OS is a ray between OP and OR.
To Prove:
$\angle ROS = \frac{1}{2} (\angle QOS – \angle POS)$
Proof:
Since OR $\perp$ PQ, we have:
$\angle POR = 90^\circ$
... (i)
$\angle ROQ = 90^\circ$
... (ii)
Consider $\angle QOS$. It is the sum of $\angle ROQ$ and $\angle ROS$.
$\angle QOS = \angle ROQ + \angle ROS$
Substituting the value from (ii):
$\angle QOS = 90^\circ + \angle ROS$
... (iii)
Consider $\angle POS$. It is the difference between $\angle POR$ and $\angle ROS$.
$\angle POS = \angle POR - \angle ROS$
Substituting the value from (i):
$\angle POS = 90^\circ - \angle ROS$
... (iv)
Now, let's subtract equation (iv) from equation (iii):
$\angle QOS - \angle POS = (90^\circ + \angle ROS) - (90^\circ - \angle ROS)$
$\angle QOS - \angle POS = 90^\circ + \angle ROS - 90^\circ + \angle ROS$
$\angle QOS - \angle POS = 2 \angle ROS$
Divide both sides by 2:
$\frac{1}{2} (\angle QOS - \angle POS) = \angle ROS$
Rearranging the terms, we get:
$\angle ROS = \frac{1}{2} (\angle QOS – \angle POS)$
Hence Proved.
Question 6. It is given that ∠ XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ ZYP, find ∠ XYQ and reflex ∠ QYP.
Answer:
Given:
$\angle$ XYZ = $64^\circ$
XY is produced to point P (XYP is a straight line).
Ray YQ bisects $\angle$ ZYP (meaning $\angle$ ZYQ = $\angle$ QYP).
To Find:
$\angle$ XYQ
Reflex $\angle$ QYP
Figure:
First, we draw a line XY and extend it to P. Then we draw a ray YZ such that $\angle$ XYZ = $64^\circ$. Finally, we draw a ray YQ that divides the angle $\angle$ ZYP into two equal angles.
Solution:
Since XYP is a straight line, the angles $\angle$ XYZ and $\angle$ ZYP form a linear pair.
Therefore, the sum of these angles is $180^\circ$.
$\angle$ XYZ + $\angle$ ZYP = $180^\circ$
(Linear Pair Axiom)
We are given $\angle$ XYZ = $64^\circ$. Substitute this value into the equation:
64$^\circ$ + $\angle$ ZYP = $180^\circ$
Subtract $64^\circ$ from both sides to find $\angle$ ZYP:
$\angle$ ZYP = $180^\circ - 64^\circ$
$\angle$ ZYP = $116^\circ$
... (i)
Ray YQ bisects $\angle$ ZYP. This means that YQ divides $\angle$ ZYP into two equal angles, $\angle$ ZYQ and $\angle$ QYP.
$\angle$ ZYQ = $\angle$ QYP = $\frac{1}{2} \angle$ ZYP
Substitute the value of $\angle$ ZYP from equation (i):
$\angle$ ZYQ = $\angle$ QYP = $\frac{1}{2} \times 116^\circ$
$\angle$ ZYQ = $\angle$ QYP = $58^\circ$
$\angle$ QYP = $58^\circ$
... (ii)
Now, we need to find $\angle$ XYQ. This angle is the sum of adjacent angles $\angle$ XYZ and $\angle$ ZYQ.
$\angle$ XYQ = $\angle$ XYZ + $\angle$ ZYQ
Substitute the given value $\angle$ XYZ = $64^\circ$ and the calculated value $\angle$ ZYQ = $58^\circ$:
$\angle$ XYQ = $64^\circ + 58^\circ$
$\angle$ XYQ = $122^\circ$
... (iii)
Finally, we need to find the reflex $\angle$ QYP. The reflex angle is the angle greater than $180^\circ$ and less than $360^\circ$. It is calculated by subtracting the angle from $360^\circ$.
Reflex $\angle$ QYP = $360^\circ - \angle$ QYP
Substitute the value of $\angle$ QYP from equation (ii):
Reflex $\angle$ QYP = $360^\circ - 58^\circ$
Reflex $\angle$ QYP = $302^\circ$
... (iv)
Answer:
$\angle$ XYQ = $122^\circ$
Reflex $\angle$ QYP = $302^\circ$
Example 4 to 6 (Before Exercise 6.2)
Example 4. In Fig. 6.19, if PQ || RS, ∠ MXQ = 135° and ∠ MYR = 40°, find ∠XMY
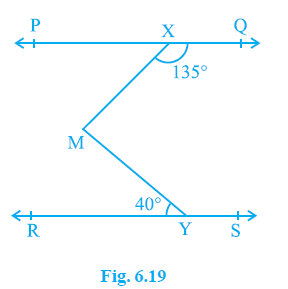
Answer:
Given:
PQ || RS
$\angle$ MXQ = $135^\circ$
$\angle$ MYR = $40^\circ$
To Find:
$\angle$ XMY
Construction Required:
Draw a line AB through point M parallel to PQ. Since PQ || RS, this line AB will also be parallel to RS.
Solution:
Since line AB || PQ and XM is a transversal line cutting these parallel lines,
The sum of consecutive interior angles is $180^\circ$.
$\angle$ MXQ + $\angle$ XMB = $180^\circ$
(Consecutive Interior Angles are supplementary)
Substitute the given value of $\angle$ MXQ = $135^\circ$:
$135^\circ + \angle$ XMB = $180^\circ$
Subtract $135^\circ$ from both sides to find $\angle$ XMB:
$\angle$ XMB = $180^\circ - 135^\circ$
$\angle$ XMB = $45^\circ$
... (i)
Since line AB || RS and MY is a transversal line cutting these parallel lines,
The alternate interior angles are equal.
$\angle$ BMY = $\angle$ MYR
(Alternate Interior Angles are equal)
Substitute the given value of $\angle$ MYR = $40^\circ$:
$\angle$ BMY = $40^\circ$
... (ii)
The angle $\angle$ XMY is the sum of the adjacent angles $\angle$ XMB and $\angle$ BMY.
$\angle$ XMY = $\angle$ XMB + $\angle$ BMY
Substitute the values from equation (i) and equation (ii):
$\angle$ XMY = $45^\circ + 40^\circ$
$\angle$ XMY = $85^\circ$
Answer:
$\angle$ XMY = $85^\circ$.
Example 5. If a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel.
Answer:
Given:
Let two lines AB and CD be intersected by a transversal XY at points Q and R respectively.
Let $\angle$ XQB and $\angle$ QRD be a pair of corresponding angles.
Let QP' be the bisector of $\angle$ XQB and RS' be the bisector of $\angle$ QRD.
It is given that QP' || RS'.
To Prove:
AB || CD.
Figure:
Draw two lines AB and CD intersected by a transversal XY. Mark points Q and R. Draw ray QP' bisecting $\angle$ XQB and ray RS' bisecting $\angle$ QRD.
Proof:
Since QP' is the bisector of $\angle$ XQB, it divides the angle into two equal halves.
$\angle$ XQP' = $\angle$ P'QB = $\frac{1}{2} \angle$ XQB
... (i)
Since RS' is the bisector of $\angle$ QRD, it divides the angle into two equal halves.
$\angle$ QRS' = $\angle$ S'RD = $\frac{1}{2} \angle$ QRD
... (ii)
We are given that the bisectors QP' and RS' are parallel (QP' || RS'), and XY is the transversal intersecting them.
When a transversal intersects two parallel lines, the corresponding angles are equal.
Thus, the corresponding angles formed by the parallel lines QP' and RS' and the transversal XY are equal:
$\angle$ XQP' = $\angle$ QRS'
(Corresponding angles, since QP' || RS')
Substitute the values from equation (i) and equation (ii) into this equality:
$\frac{1}{2} \angle$ XQB = $\frac{1}{2} \angle$ QRD
Multiply both sides by 2:
$\angle$ XQB = $\angle$ QRD
The angles $\angle$ XQB and $\angle$ QRD are a pair of corresponding angles formed by the transversal XY intersecting the lines AB and CD.
Since the corresponding angles are equal ($\angle$ XQB = $\angle$ QRD), by the converse of the Corresponding Angles Axiom, the lines AB and CD must be parallel.
Thus, AB || CD.
Hence Proved.
Example 6. In Fig. 6.22, AB || CD and CD || EF. Also EA⊥AB. If ∠BEF = 55°, find the values of x, y and z.

Answer:
Given:
AB || CD
CD || EF
EA ⊥ AB, which means $\angle$ EAB = $90^\circ$.
$\angle$ BEF = $55^\circ$
BE intersect CD at point D.
Extend AB and CD to point B' and D' respectively.
The angles are labelled in the figure as $\angle$ EBB' = x, $\angle$ EDD' = y, and $\angle$ AEB = z.
To Find:
The values of x, y, and z.
Solution:
We are given that CD || EF and ED is a transversal intersecting these parallel lines.
The sum of the interior angles on the same side of the transversal is $180^\circ$.
From the figure and the given information in the question, we can see that $\angle$ EDD' (which is y) and $\angle$ DEF are interior angles on the same side of transversal ED.
y + 55$^\circ$ = $180^\circ$
(Interior angles on the same side of the transversal ED)
Subtract $55^\circ$ from both sides to find y:
y = $180^\circ - 55^\circ$
y = $125^\circ$
... (i)
Now, we are given that AB || CD and ED is a transversal.
x = y
(Corresponding Angles)
Since y = $125^\circ$ from equation (i):
x = $125^\circ$
... (ii)
We are given that AB || CD and CD || EF.
By the property of parallel lines (transitivity), if two lines are parallel to the same line, they are parallel to each other.
Therefore, AB || EF.
Now consider parallel lines AB || EF and transversal EA intersecting them.
The sum of the interior angles on the same side of the transversal is $180^\circ$.
$\angle$ EAB + $\angle$ AEF = $180^\circ$
(Interior angles on the same side of the transversal EA)
We are given $\angle$ EAB = $90^\circ$. From the figure, $\angle$ AEF is composed of two adjacent angles, $\angle$ AEB and $\angle$ BEF. The figure labels $\angle$ AEB as z and $\angle$ BEF as $55^\circ$. So, $\angle$ AEF = $\angle$ AEB + $\angle$ BEF = z + $55^\circ$.
Substitute these values into the interior angles equation:
90$^\circ$ + (z + 55$^\circ$) = $180^\circ$
Simplify the equation:
90$^\circ$ + z + 55$^\circ$ = $180^\circ$
z + 145$^\circ$ = $180^\circ$
Subtract $145^\circ$ from both sides to find z:
z = $180^\circ - 145^\circ$
z = $35^\circ$
... (iii)
Answer:
The values are:
x = $125^\circ$
y = $125^\circ$
z = $35^\circ$
Exercise 6.2
Question 1. In Fig. 6.23, if AB || CD, CD || EF and y : z = 3 : 7, find x.

Answer:
Given:
AB || CD
CD || EF
$y : z = 3 : 7$
To Find:
The value of x.
Solution:
We are given that AB || CD and CD || EF.
If two lines are parallel to the same line, then they are parallel to each other.
Therefore, AB || EF.
Since CD || AB and the transversal intersects them, the angles x and y are consecutive interior angles on the same side of the transversal.
The sum of consecutive interior angles is $180^\circ$.
$y + x = 180^\circ$
(Consecutive Interior Angles) ...(i)
Since AB || EF and the transversal intersects them, the angles x and z are alternate interior angles.
Alternate interior angles are equal when lines are parallel.
$x = z$
(Alternate Interior Angles, since AB || EF) ...(ii)
From eq (i) and (ii), we get:-
$y + z = 180^\circ$
We are given the ratio $y : z = 3 : 7$. Let $y = 3k$ and $z = 7k$ for some constant k.
Substitute these values into the equation $y + z = 180^\circ$:
$3k + 7k = 180^\circ$
$10k = 180^\circ$
Divide both sides by 10:
$k = \frac{180^\circ}{10}$
$k = 18^\circ$
Now, we can find the values of y and z:
$y = 3k = 3 \times 18^\circ = 54^\circ$
$z = 7k = 7 \times 18^\circ = 126^\circ$
Substitute the value of z that we found:
$x = 126^\circ$
Answer:
The value of x is $126^\circ$.
Question 2. In Fig. 6.24, if AB || CD, EF⊥CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.
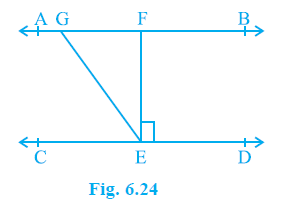
Answer:
Given:
AB || CD
EF ⊥ CD
$\angle$GED = $126^\circ$
To Find:
$\angle$AGE, $\angle$GEF and $\angle$FGE
Solution:
We are given that AB || CD and GD is a transversal intersecting AB and CD.
$\angle$AGE = $\angle$GED
(Alternate Interior Angles)
Substitute the given value of $\angle$GED:
$\angle$AGE = $126^\circ$
So, $\angle$AGE = $126^\circ$.
We are given that EF ⊥ CD. This means that $\angle$FED = $90^\circ$.
From the figure, we can see that $\angle$GED is the sum of $\angle$GEF and $\angle$FED.
$\angle$GED = $\angle$GEF + $\angle$FED
Substitute the known values:
$126^\circ$ = $\angle$GEF + $90^\circ$
Now, solve for $\angle$GEF:
$\angle$GEF = $126^\circ - 90^\circ$
$\angle$GEF = $36^\circ$
So, $\angle$GEF = $36^\circ$.
Now, consider the straight line AB. The angles $\angle$AGE and $\angle$FGE form a linear pair.
$\angle$AGE + $\angle$FGE = $180^\circ$
(Linear Pair Axiom)
Substitute the value of $\angle$AGE which we found to be $126^\circ$:
$126^\circ$ + $\angle$FGE = $180^\circ$
Now, solve for $\angle$FGE:
$\angle$FGE = $180^\circ - 126^\circ$
$\angle$FGE = $54^\circ$
So, $\angle$FGE = $54^\circ$.
Final Answer:
$\angle$AGE = $126^\circ$
$\angle$GEF = $36^\circ$
$\angle$FGE = $54^\circ$
Question 3. In Fig. 6.25, if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.
[Hint: Draw a line parallel to ST through point R.]
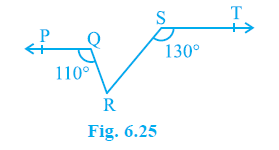
Answer:
Given:
PQ || ST
$\angle$PQR = $110^\circ$
$\angle$RST = $130^\circ$
To Find:
$\angle$QRS
Construction Required:
Draw a line XY through point R such that XY is parallel to ST. Since PQ || ST is given, it follows that XY will also be parallel to PQ (Lines parallel to the same line are parallel to each other).
Solution:
Consider PQ || XY and QR as a transversal.
The angles $\angle$PQR and $\angle$QRX are consecutive interior angles.
$\angle$PQR + $\angle$QRX = $180^\circ$
(Sum of consecutive interior angles is $180^\circ$)
Substitute the given value $\angle$PQR = $110^\circ$:
110$^\circ$ + $\angle$QRX = $180^\circ$
$\angle$QRX = $180^\circ - 110^\circ$
$\angle$QRX = $70^\circ$
... (i)
Now, consider ST || XY and SR as a transversal.
The angles $\angle$RST and $\angle$SRY are consecutive interior angles.
$\angle$RST + $\angle$SRY = $180^\circ$
(Sum of consecutive interior angles is $180^\circ$)
Substitute the given value $\angle$RST = $130^\circ$:
130$^\circ$ + $\angle$SRY = $180^\circ$
$\angle$SRY = $180^\circ - 130^\circ$
$\angle$SRY = $50^\circ$
... (ii)
Since XY is a straight line, the angles on the line at point R sum up to $180^\circ$.
$\angle$QRX + $\angle$QRS + $\angle$SRY = $180^\circ$
(Angles on a straight line)
Substitute the values from (i) and (ii):
70$^\circ$ + $\angle$QRS + 50$^\circ$ = $180^\circ$
120$^\circ$ + $\angle$QRS = $180^\circ$
$\angle$QRS = $180^\circ - 120^\circ$
$\angle$QRS = $60^\circ$
Final Answer:
The value of $\angle$QRS is $60^\circ$.
Question 4. In Fig. 6.26, if AB || CD, ∠ APQ = 50° and ∠ PRD = 127°, find x and y.

Answer:
Given:
AB || CD
$\angle$APQ = $50^\circ$
$\angle$PRD = $127^\circ$
To Find:
Values of x and y.
Solution:
We are given that AB || CD and PQ is a transversal line intersecting AB and CD.
The angle $\angle$APQ and $\angle$PQR (which is x) are alternate interior angles.
$\angle$APQ = $\angle$PQR
(Alternate Interior Angles)
Substitute the given value $\angle$APQ = $50^\circ$ and $\angle$PQR = x:
$50^\circ$ = x
So, x = $50^\circ$.
Now, consider AB || CD and PR as a transversal line intersecting AB and CD.
The angle $\angle$APR and $\angle$PRD are alternate interior angles.
$\angle$APR = $\angle$PRD
(Alternate Interior Angles)
From the figure, $\angle$APR is the sum of $\angle$APQ and $\angle$QPR (which is y).
$\angle$APQ + $\angle$QPR = $\angle$PRD
Substitute the given values $\angle$APQ = $50^\circ$, $\angle$QPR = y, and $\angle$PRD = $127^\circ$:
50$^\circ$ + y = $127^\circ$
Now, solve for y:
y = $127^\circ - 50^\circ$
y = $77^\circ$
So, y = $77^\circ$.
Final Answer:
x = $50^\circ$ and y = $77^\circ$.
Question 5. In Fig. 6.27, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.

Answer:
Given:
PQ and RS are two mirrors placed parallel to each other, so PQ || RS.
AB is the incident ray on mirror PQ at point B.
BC is the reflected ray from PQ and the incident ray on mirror RS at point C.
CD is the reflected ray from mirror RS.
To Prove:
AB || CD
Construction Required:
Draw a line BM perpendicular to mirror PQ at point B.
Draw a line CN perpendicular to mirror RS at point C.
Proof:
According to the Law of Reflection, the angle of incidence is equal to the angle of reflection.
At mirror PQ, AB is the incident ray and BC is the reflected ray. BM is the normal (perpendicular) to PQ at B.
$\angle$ ABM = $\angle$ MBC
(Angle of incidence = Angle of reflection at mirror PQ)
At mirror RS, BC is the incident ray and CD is the reflected ray. CN is the normal (perpendicular) to RS at C.
$\angle$ BCN = $\angle$ NCD
(Angle of incidence = Angle of reflection at mirror RS)
We are given that the mirrors PQ and RS are parallel (PQ || RS).
Since BM is perpendicular to PQ and CN is perpendicular to RS, and PQ || RS, it means that BM and CN are also parallel to each other.
BM || CN
(Normals to parallel lines are parallel)
Now consider the parallel lines BM and CN, and the transversal line BC intersecting them.
The angles $\angle$ MBC and $\angle$ BCN are alternate interior angles formed by the transversal BC.
When two parallel lines are intersected by a transversal, the alternate interior angles are equal.
$\angle$ MBC = $\angle$ BCN
(Alternate Interior Angles, since BM || CN) ... (i)
Now let's consider the angles $\angle$ ABC and $\angle$ BCD.
The angle $\angle$ ABC is the sum of the adjacent angles $\angle$ ABM and $\angle$ MBC.
$\angle$ ABC = $\angle$ ABM + $\angle$ MBC
Since $\angle$ ABM = $\angle$ MBC (Law of Reflection at PQ), we can write:
$\angle$ ABC = $\angle$ MBC + $\angle$ MBC
$\angle$ ABC = 2 $\angle$ MBC
... (ii)
The angle $\angle$ BCD is the sum of the adjacent angles $\angle$ BCN and $\angle$ NCD.
$\angle$ BCD = $\angle$ BCN + $\angle$ NCD
Since $\angle$ BCN = $\angle$ NCD (Law of Reflection at RS), we can write:
$\angle$ BCD = $\angle$ BCN + $\angle$ BCN
$\angle$ BCD = 2 $\angle$ BCN
... (iii)
From equation (i), we know that $\angle$ MBC = $\angle$ BCN.
Substitute this into equation (ii) and equation (iii):
$\angle$ ABC = 2 $\angle$ MBC
$\angle$ BCD = 2 $\angle$ BCN = 2 $\angle$ MBC
Comparing the expressions for $\angle$ ABC and $\angle$ BCD, we see that they are equal.
$\angle$ ABC = $\angle$ BCD
These angles, $\angle$ ABC and $\angle$ BCD, are alternate interior angles formed by the transversal BC intersecting the lines AB and CD.
Since the alternate interior angles are equal, by the converse of the Alternate Interior Angles Theorem, the lines AB and CD must be parallel.
Therefore, AB || CD.
Hence Proved.

